從浴廁龍頭濺灑的水珠、下雨的雨滴、噴墨印刷的墨珠到各種藥劑噴霧，液滴普遍存在於我們生活和工業製程的各個角落。相對於附著在固體表面上的黏著液滴，懸浮液滴是不與任何固體接觸、只被不互溶流體包圍的液滴。在無重力的環境中達靜力平衡時，懸浮液滴是完美的圓球。而這種液滴的共振現象的研究發展，是本系列文章的主題。
懸浮液滴共振現象的研究始於1879年Rayleigh的理論。該理論探討球狀、無黏性的懸浮液滴在真空中的自然振盪，預測了一系列的軸對稱模態和它們的頻率[1]。半世紀後，Lamb於1932年推廣了Rayleigh的理論，考慮兩種不互溶、無黏性流體間球狀介面的線性共振，進一步預測了球狀介面的非軸對稱模態[2]。Rayleigh和Lamb的懸浮液滴理論在二十世紀前半似乎並未受到重視，但時至今日，這些理論已然成為與液滴共振相關的研究必定引數的經典之作。
根據Lamb的理論，球狀懸浮液滴共振模態的形狀s(θ,φ)是球面與球諧函數與的疊加

其中，r為介面半徑、θ和φ分別是球座標的緯度角和經度角，ε是球狀介面的變形量，數值很小，P_k^l (sinθ)是k次、l階的associatedLegendrefunction。以下，液滴的模態將以數對[k,l]代稱。圖一呈現了液滴的三種共振模態。首先，zonal模態的階數l為零。這種模態沒有經度方向的波，液滴形狀將呈現軸對稱。譬如圖中的[4,0]模態，我們只看到五層緯度方向的軸對稱波形，這也是Reyleigh第一個理論模型能預測的範疇。其次，sectoral模態的次數k等於階數l，液滴將是單層、多扇的旋轉對稱波形。譬如圖中的[4,4]模態具有單層、四扇經度方向的波形。最後，tesseral模態滿足k > l > 0，形狀是多層、多扇的旋轉對稱波形。譬如圖中的[4,2]模態是兩扇、三層的波形，[4,3]則為三扇、兩層。
根據Lamb的理論，球狀介面的自然振盪頻率是

其中，σ是介面的表面張力，ρi和ρo則分別是介面內、外部流體的密度。由此，Lamb的理論不但包含了懸浮液滴在空氣中的振盪行為，也能預測氣泡和液滴於不互溶液體中的共振現象。而當我們令ρo為零，化簡後就是Reyleigh預測的、真空中懸浮液滴的自然頻率。值得注意的是，依照Lamb的理論，球狀液滴的共振頻率只跟次數k有關，所以次數k相同的模態（同次模態）會以相同頻率振盪[2]。譬如，[2, 0]、 [2, 1]和[2, 2]的振盪頻率相同，而[3, 0]、[3, 1]、[3, 2]和[3, 3]的頻率也相同。同理，圖一中的五個模態也會用一樣的頻率振盪。如此一來，我們是不是就不可能在實驗中各別觸發、觀察到這些模態了呢？

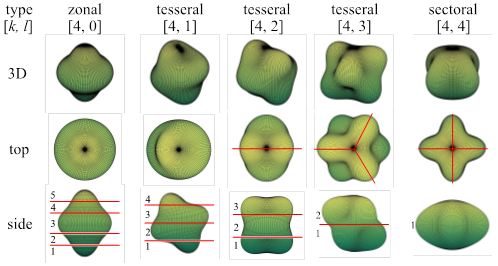█ 圖一、以幾何形狀辨別懸浮液滴的共振模態。參數k和l分別為associated Legendre function P_k^l (cosθ)的次數和階數。Sectoral和tesseral模態可由上視圖（top）中的幾何特徵分割成旋轉對稱的扇狀結構；所有模態可依側視圖（side）中的節圓分割成層狀結構。

儘管懸浮液滴理想化（無黏性、球狀介面和小振幅線性振盪）的共振行為早在一百四十年前就被預測，但地球的重力為製造完美球型的懸浮液滴、進而實驗量測驗證帶來各種技術挑戰。據筆者所知，最早的相關結果似乎是1944年Kornfeld和Suvorov發表的氣泡空蝕（cavitation）實驗。該學者以電磁線圈驅動浸泡在液體中的鎳圓管高頻振盪，藉此產生氣泡。鎳管振幅較小時，作者拍到共振氣泡的俯視照片，其氣泡的形狀似乎就是Lamb所預測的sectoral模態[3]。接著，Holter無意間在實驗中觀察到懸浮液滴的許多共振模態，並在1952年與Glasscock一同發表相關結果，希望引起相關領域學者的興趣[4]。圖二節錄了該論文部分實驗照片。

█ 圖二、幾個Holter和Glasscock觀察到的懸浮液滴共振模態 [4]。

Rayleigh發表1879年懸浮液滴共振理論的往後一百年間，似乎沒有學者著手進行仔細的實驗觀測。再一次地，地球的重力為製造完美球型的懸浮液滴帶來各種技術挑戰。一直等到超音波、電場等製造懸浮液滴的實驗方法被提出之後，相關的量化實驗才得以順利進行。就此，地球的重力把近代的懸浮液滴實驗整整推遲了一百年。

參考文獻
1.Strutt John, W., VI. On the capillary phenomena of jets. Proceedings of the Royal Society of London,
1879. 29(196-199): p. 71-97.
2.Lamb,H., Hydrodynamics. 1932, New York: Dover publications.
3.Kornfeld, M. and L. Suvorov, On the destructive action of cavitation. Journal of Applied Physics, 1944.
15(6): p. 495-506.
4.Holter, N.J. and W.R. Glasscock, Vibrations of Evaporating Liquid Drops. Journal of the Acoustical
Society of America, 1952. 24(6): p. 682-686.
5.Trinh, E. and T.G. Wang, Large-Amplitude Free and Driven Drop-Shape Oscillations - Experimental-
Observations. Journal of Fluid Mechanics, 1982. 122(Sep): p. 315-338.
6.Trinh, E., A. Zwern, and T.G. Wang, An Experimental-Study of Small-Amplitude Drop Oscillations in
Immiscible Liquid-Systems. Journal of Fluid Mechanics, 1982. 115(Feb): p. 453-474.
7.Trinh, E.H., R.G. Holt, and D.B. Thiessen, The dynamics of ultrasonically levitated drops in an electric
field. Physics of Fluids, 1996. 8(1): p. 43-61.
8.Trinh, E.H., D.B. Thiessen, and R.G. Holt, Driven and freely decaying nonlinear shape oscillations of
drops and bubbles immersed in a liquid: Experimental results. Journal of Fluid Mechanics, 1998. 364: p.
253-272.
9.Shen, C.L., W.J. Xie, and B. Wei, Parametrically excited sectorial oscillation of liquid drops floating in
ultrasound. Physical Review E, 2010. 81(4).
10.Marston, P.L. and R.E. Apfel, Acoustically Forced Shape Oscillation of Hydrocarbon Drops Levitated in
Water. Journal of Colloid and Interface Science, 1979. 68(2): p. 280-286.
11.Feng, J.Q. and K.V. Beard, 3-Dimensional Oscillation Characteristics of Electrostatically Deformed
Drops. Journal of Fluid Mechanics, 1991. 227: p. 429-447.
12.Suryanarayana, P.V.R. and Y. Bayazitoglu, Effect of Static Deformation and External Forces on the
Oscillations of Levitated Droplets. Physics of Fluids a-Fluid Dynamics, 1991. 3(5): p. 967-977.