「哈利波特低頭望著那窩蛋，注意到那枚在其他水泥色龍蛋中閃爍發光的金蛋，就擱在龍的兩隻前腿中間。『好，』哈利告訴自己，『就用聲東擊西戰術……我們走……』」
「你們現在低頭看看手裡的金蛋，就會發現它其實是可以打開來的……看到那兒的接縫了嗎？你們必須解開藏在金蛋裡的線索—它會告訴你們第二項任務的內容，你們可以事先做好準備！」
—J. K. 羅琳《哈利波特：火盃的考驗》〈第一項任務〉

請設計一承載薄殼結構，滿足以下規格和要求：
1. 結構為一密閉容器，內部裝有密度約為1.03 g/cm3的水分和營養物質，此內容物不能流出。
2. 薄殼內有微小孔洞連接內外，使得高溫時（約37 °C）外部的氧氣可以擴散進入容器、內部的水分與反應生成之二氧化碳可以擴散到大氣。
3. 必須能長時間承受自身重量（含內容物）幾十倍的重物擠壓，而不破裂或損壞。
4. 薄殼必須可以從內部破壞，使得容器內部的物體在必要時可以破殼而出。
5. 殼厚分布必須均勻，同一容器的厚度差異應在10%以下。
6. 具有低成本、高良率的製造方法
7. 有許多型號可供選擇，例如：尺寸從10mm到150mm；重量從0.3克到1500 克；形狀有球形、橢球形、蛋形、梨形（pyriform）、對稱及不對稱；顏色有純白、淺藍、深綠、紅色、無花紋、有花紋、斑點、條紋、單色及多色。
上述的「產品」直到今日仍然沒有工程方法能製造出來。但這樣的「產品」已存在地球上超過一億年，大自然在演化過程中隨機「設計製造」出來的－蛋殼。

█ 論文中有取得實驗樣本的40多種物種中的14種。左起：栗喉蜂虎、白尾八哥、鵪鶉、鴿子、紅腹錦雞、金剛鸚鵡、藍腹鷴、火雞、藍孔雀、黑腳企鵝、鵝、丹頂鶴、鴯鶓、鴕鳥（比例尺：100 mm；樣本來源：台北市立動物園，均為未受精蛋或是族群管理考量而無繁殖需求的物種）

科學家現在相信，我們身邊的所有現代鳥類（後文簡稱鳥類），包括你家門口的麻雀到冰箱裡的全雞，都是恐龍的直系後裔。暴龍和鳥類的血緣關係甚至比暴龍跟梁龍來的近。鳥類超過1萬種，其體型大小、生活型態均有極大的差異。鳥類於白堊紀時曾與其他中生代鳥類，如反鳥亞綱（Enantiornithes）、黃昏鳥目（Hesperornithes），以及非鳥恐龍（nonaviandinosaurs）並存於地球上，但恐龍與中生代古鳥類於6千6百萬年前的K-Pg大滅絕事件消失在地球上，而鳥類不僅存活下來，還成功散布全球（avianradiation）。恐龍和鳥類都是卵生，恐龍蛋孵化期相當長（某些鳥盤目恐龍可達5.8個月）。相對而言，鳥蛋的孵化期很短，大約在11天（如杜鵑）到77天（如信天翁）之間。此外，鳥蛋相對較大、每窩蛋的數目較少。鳥蛋孵化期得以縮短的一個重要原因是鳥類創新的「接觸孵蛋」。接觸孵蛋意指親鳥腹部與巢中的蛋直接接觸，藉由體溫將蛋維持在一個較高的孵化溫度。而恐龍則是像其他現存爬蟲類，僅將產下的蛋用沙土覆蓋，不主動孵蛋或照顧，至於孵化後能否存活，就只能聽天由命了（科學界一般認為恐龍沒有接觸孵蛋，但仍有爭議，由於出土的恐龍蛋化石極少，證明這一點的難度很高）。接觸孵蛋使得鳥類的孵化期得以縮短、減少受掠食的機會，增加後代的存活率。然而，接觸孵蛋的「成本」很高，親鳥於孵化期間必須日夜無休的孵蛋，除了覓食時間受限，也較易受掠食者捕食。
一個極端的例子就是皇帝企鵝（Aptenodytes forsteri），在南極大陸攝氏零下57度的低溫下，公企鵝將蛋放置在兩腿之間保暖，連續64天直到孵化。當蛋終於孵化時，公企鵝往往已超過115天未進食。倫敦自然史博物館從超過七百萬件館藏中精挑細選出22件展品，於一間名為「寶藏」（Treasures）的常設展廳展示。這些展品包括達爾文《物種起源》初版書、一具始祖鳥化石、一隻已絕種大海雀（GreatAuk）的剝製標本、一塊月球表面岩石、一個尼安德塔人頭顱。其中一件略顯平凡的展品：一個巨大鳥蛋，約有13公分長，這是一顆皇帝企鵝的蛋。這顆企鵝蛋是英國皇家海軍軍官暨探險家史考特（RobertFalconScott）1911年那趟悲劇性南極探險的收穫。皇帝企鵝產卵、孵化的地點在南極大陸上一處最偏遠的地方，時間是南半球冬季最嚴寒之時。他們一行人在接近全黑的環境中、步行100多公里，到達南極洲內陸的繁殖地克羅澤角（CapeCrozier）。史考特和其他兩位夥伴死在結凍的營帳中，唯一的倖存者薛瑞葛拉德（ApsleyGeorgeBebetCherry-Garrard）將採集到的3顆蛋（另有2顆在回程途中毀損）交給自然史博物館。這段經歷記述於1922年出版的《世界最險惡之旅》（TheWorstJourneyintheWorld）一書中。書中有句常被引用的嘲諷句子：「在人類設計來自我折磨的方法中，極地探險是最乾淨也最孤獨的方式了。」而皇帝企鵝竟能在這「世界最險惡」的地方生存繁衍－鳥蛋的繁衍方式到底是幫忙，還是幫倒忙?
另一個因接觸孵蛋而導致的問題就是，蛋殼的「機械設計」變得重要，且具有互相矛盾的設計要求—不能太薄，以免接觸孵蛋時因碰撞或是親鳥負載而破裂；同時也不能太厚，以免雛鳥無法破殼而出。鳥蛋的大小、形狀、顏色差異極大，例如已滅絕的象鳥重達450公斤（Aepyornismaximus，蛋重9000克）；而現存的蜂鳥僅有3克（Mellisugaminima，蛋重0.3克），兩者相差五個數量級。這些大小形狀差異極大的鳥蛋是否存在某種力學上的「設計準則」?
儘管多年來文獻中已有許多鳥蛋相關的研究，但令人意外的是，人們對鳥蛋的「設計」奧秘仍不完全清楚。今年2017年6月23日著名的《科學》（Science）刊登了一篇封面論文[1]，即在探討鳥蛋的形狀，作者分析了鳥綱下所有37個目，共計49,175顆蛋的照片（取自TheMuseumofVertebrateZoologyat Berkeley），發現鳥蛋的形狀似乎和鳥類的飛行能力有關連¾飛行能力愈好的鳥類，其鳥蛋愈不對稱，也愈橢圓，但背後的因果關係仍不清楚。該論文沒有觸及，但也相同重要的問題是，作為承載薄壁結構（Load-bearingthin-walledstructure）的蛋殼，影響其剛度的重要參數，如鳥蛋大小、蛋殼厚度、蛋殼的楊氏係數（Young'smodulus）又存在著什麼規律? 若給定某一鳥重，是否能決定其鳥蛋的「適當」剛度，以及其對應的大小、殼厚與材料呢?（若將鳥蛋近似為一根彈簧，則蛋的剛度，或稱為勁度，約略等同於彈簧的彈性常數。）回答這個問題的挑戰在於，薄殼結構的剛度與大小、殼厚、材料與形狀都有關，而不同物種的鳥蛋差異極大，難以互相比較。例如：象鳥蛋的剛度雖遠大於蜂鳥蛋，但是否夠大到足以支撐巨大的象鳥體重?
為回答這個問題，我們與台北市立動物園合作，過去三年分析了鳥重橫跨5個數量級、分屬36個目的463個物種，研究結果發表在自然出版集團的期刊《ScientificReports》[2]。
我們定義了一個無因次參數Cnumber來量化鳥蛋的剛度。Cnumber有幾個特別之處：(1)Cnumber為蛋的剛度、蛋重、長短軸的簡單函數，僅有數字而無單位，故不同物種間大小差異極大的鳥蛋得以互相比較；(2)計算Cnumber所需的參數很容易量測，剛度由機械實驗常用的壓縮試驗機量得，蛋重和長短軸長則僅需一般的電子秤和游標卡尺；(3)Cnumber的物理意義為鳥蛋在除去大小與形狀的影響之後的相對剛度值。如前所述，蛋殼剛度是大小、形狀、殼厚、蛋殼材料的函數，此函數可由薄殼理論得到，將剛度的函數代入Cnumber化簡後得到C與蛋殼的楊氏係數以及殼厚平方成正比，而與蛋重成反比。若某蛋的Cnumber較大，表示其剛度相對於蛋重而言偏大（由於殼厚或者楊氏係數偏大所致）。

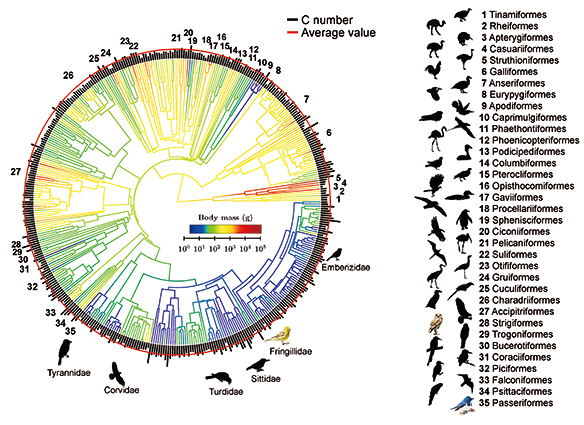█ 416種鳥類的譜系圖。圓心為現代鳥類的共祖，距今約為1億多年前，圓周上每個黑色線條代表一個物種，圓心到圓周的分岔代表演化過程的分化。黑色線條的長度為C number（線性尺度）、分岔線條的顏色代表鳥重（對數尺度），紅圈為 C number 的平均值。

我們從台北市立動物園取得40多種、共計500多顆剛產下的鳥蛋樣本進行實驗。（這些蛋均為未受精蛋或是族群管理考量而無繁殖需求的物種。）此外，我們也建立了一套電腦模擬的方法，使用文獻和博物館的鳥蛋照片及數據，在電腦中模擬壓縮實驗的過程，計算出分屬36個目、104科、約430種鳥類的Cnumber。使用這套電腦模擬方法可將研究範圍大幅擴展到許多無法取得新鮮鳥蛋樣本的物種、甚至是已滅絕的物種（例如象鳥）。有趣的是，分析上千顆蛋之後，發現絕大多數物種的Cnumber都落在15,000左右，且實驗與模擬得到一致的結果。因此C=15000可視為鳥蛋機械設計的「準則」－蛋重、殼厚和蛋殼楊氏係數必須滿足這個關係，才算是「正常」的蛋，偏高和偏低都表示該鳥類可能有獨特的繁殖策略。Cnumber顯著偏低的物種有奇異鳥（Apteryxaustralis）、塚雉（Macrocephalonmaleo）和信天翁（Diomedeaexulans）。這三種鳥都有獨特的繁殖策略，奇異鳥的蛋異常的大，大約為鳥重的20%（一般約為5%）；塚雉則是唯一不使用接觸孵蛋，而是將蛋埋在沙土之中，透過環境溫度孵蛋的鳥類；信天翁則是孵化期非常長（77天，相較於雞的21天、鴕鳥的40天）。另外，我們將鳥重及Cnumber的數據放在基因定序得到的譜系圖上，發現現代鳥類可追溯到一億多年前的共祖（圓心），逐漸演化成現今的1萬多個物種（圓周），這過程鳥重的演化相當多元，但Cnumber都大致維持一個定值。顯示這個「設計準則」在演化過程中一直被保留著，不隨鳥重的變化而變化。
類似的不變量在自然界中並不少見，例如：大型動物的排尿時間[3]、生材的楊氏係數與密度的比值[4]，以及動物跳躍的高度[5]等均大致為定值。這些不變量的存在乃是由於生物體受到地球強大的重力作用而演化出的「最佳設計」。雖然個別物種與大趨勢有所偏離，但若考慮許多物種，體重橫跨好幾個數量級時，這些「設計準則」往往被準確的遵循著。
此研究開始於2014年9月，最初進行研究的是大三專題生陳品衣，一切從零開始，憑藉著一股好奇心探索未知。從嘗試性的初步測試、猜想可能的「設計準則」為何，以及Cnumber要如何定義，到獲得科技部大專學生研究計畫（MOST104-2815-C-002-141）的補助、獲得學生論文競賽第二名（2015年全國力學會議學術研討會）。品衣前年大學畢業後到美國麻省理工學院（MIT）攻讀研究所，本研究由碩士生楊達璋、顏安與吳尚平接手。達璋和顏安已於去年8月完成碩士論文，現分別為研發替代役工程師與日本名古屋大學國際交換生。達璋做了大部分的模擬和實驗，他和品衣對本論文的貢獻相同。論文的另一位作者為台北市立動物園鳥園區長謝欣怡助理研究員。此研究活用課堂所學的力學理論與材料試驗的工具，除了了解大自然的奧秘、欣賞大自然之美之外，也希望能為鳥類保育，以及仿生材料的研發有所貢獻。

誌謝
感謝科技部補助陳品衣大專學生研究計畫（104-2815-C-002-141)；台北市立動物園提供剛產下的鳥蛋樣本、台大森林系袁孝維教授提供栗喉蜂虎蛋樣本；動物園王韋政、台大機械系陳湘鳳教授、莊蘇菲協助運送樣本；台大機械系許麗教授與周元昉教授提供寶貴的建議；台大材料系廖沂嘉和王成協助壓縮實驗；台大化學系佘瑞琳教授、台大化工系徐曉萍協助材料量測；英國Instituteof Zoology, ZoologicalSocietyofLondon的蘇珊博士提供寶貴的鳥類資訊與建議；台大圖書館劉應琳協助提供文獻及書籍；新加坡的MichaelToh 博士提供精美的鳥類照片。

█ 作者於壓縮試驗機前合影，左起：陳品衣、吳尚平、楊達璋及莊嘉揚教授。（照片中的樣本為鴕鳥蛋）

作者簡介：
莊嘉揚教授自加州柏克萊大學取得機械博士後，曾在美國矽谷、世界上最大的資料儲存公司威騰電子（Western Digital）從事研發多年。期間有多項專利用於今天的硬碟產品中。回到母系任教後，致力於多尺度力學與結構的研究，目前著重於薄膜材料與生物材料方面。團隊自行設計架設了一套多功能大氣電漿系統，可在大氣下鍍製光電性質良好且均勻的大面積透明導電薄膜，可用於顯示器或太陽能面板的電極。生物材料方面，設計架設了一套雷射光鉗系統，可施加或量測pN到100pN等級的微小力，進而結合光鉗與介電泳，量測微奈米粒子及生物粒子的表面特性。另外，團隊與台北市立動物園合作，探索鳥蛋機械設計之謎。在分析了鳥重橫跨5個數量級、分屬36目的463個物種之後，發現鳥蛋作為承載薄殼結構，的確存在「設計準則」—若給定鳥重，其蛋重、殼厚和蛋殼楊氏係數滿足一個簡單關係，這個簡單關係（定義為C number）可視為鳥類一億多年來演化而來的「最佳設計」，既可支撐親鳥重，也不致浪費材料。這項研究發表在自然出版集團的期刊Scientific Reports。
   曾獲得科技部吳大猷紀念獎、中華民國力學學會年輕力學學者獎、台大機械系教學貢獻獎、工研院機械所績優計畫主持人、Journal of Alloys and Compounds期刊的年度傑出審查者。現任多個國際期刊編輯、獲選為電機電子工程師學會（IEEE）的資深會員（Senior Member）。現任財團法人知遠研究發展基金會董事、曾任中華民國自動化科技學會副秘書長。曾開設的課程有靜力學、材料力學、高等材料力學、有限元素法、微機電系統設計、精密機械概論，以及創新設計學院（D-School）的設計思考入門、全球創新的原理與實踐。

延伸閱讀
[1]M. C. Stoddard, E. H. Yong, D. Akkaynak, C. Sheard, J. A. Tobias, and L. Mahadevan, “Avian egg
shape: Form, function, and evolution,” Science, vol. 356, no. 6344, pp. 1249–1254, 2017.
[2]J.-Y. Juang, P.-Y. Chen, D.-C. Yang, S.-P. Wu, and H.-I. Hsieh, “The avian egg exhibits general
allometric invariances in mechanical design,” Sci. Rep., pp. 1–11, 2017.
[3]P. J. Yang, J. Pham, J. Choo, and D. L. Hu, “Duration of urination does not change with body size.,”
Proc. Natl. Acad. Sci. U. S. A., vol. 111, no. 33, pp. 11932–11937, Jun. 2014.
[4]T. Mcmahon, “Size and shape in biology,” Science, vol. 179, no. 1973, pp. 1201–1204, 1973.
[5]T. A. McMahon and J. T. Bonner, On Size and Life, 1st editio. Scientific American Books - W. H.
Freeman & Co., 1983.